Surds are irrational numbers that cannot be written as the ratio of two integers. They are often represented by the square root symbol, such as 
Surds have some interesting properties and applications in mathematics, especially in geometry and algebra.
One way to understand surds is to compare them with rational numbers. Rational numbers are numbers that can be written as the ratio of two integers, such as 
Rational numbers can be expressed as terminating or repeating decimals, such as 0.5, 0.75, or 0.777… Surds, on the other hand, cannot be written as the ratio of two integers, and their decimal expansions are non-terminating and non-repeating, such as 1.414213…, 1.732050…, or 2.236067…
Another way to understand surds is to think of them as the roots of certain equations that have no rational solutions. For example, the equation x2 = 2 has no rational solutions, because there is no rational number that when squared gives 2. However, there is an irrational number that satisfies this equation, and that is
Similarly, the equation x2 = 3 has no rational solutions, but it has an irrational solution 
Surds are often the solutions of equations that involve square roots, cube roots, or higher-order roots.
Surds have some laws that govern their operations and simplifications. Here are some of the most common laws of surds:
– The product rule:
– The quotient rule:
– The power rule:
– The rationalization rule:
These laws can be used to simplify surds or to perform calculations with them. For example, using the product rule, we can simplify the following square root of 18 as follows
Using the quotient rule, we can simplify 
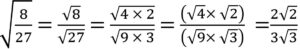
Using the power rule, we can simplify
Using the rationalization rule, we can simplify 
These are some of the basic concepts and laws of surds. Surds are useful for expressing exact values of certain quantities that cannot be measured exactly with rational numbers, such as the length of the diagonal of a square, the area of a circle, or the volume of a sphere. Surds also appear in many formulas and equations in mathematics and science, such as the Pythagorean Theorem, the quadratic formula, or the trigonometric functions.
